Chứng minh bất đẳng thức bằng phương pháp đổi biến
- Lý thuyết cơ bản chứng minh bất đẳng thức
- Lời khuyên bổ ích khi học bất đẳng thức
- Phương pháp biến đổi tương đương chứng minh bất đẳng thức
- Ứng dụng bất đẳng thức để giải phương trình
- Một số bất đẳng thức phụ hay dùng
- Chọn điểm rơi trong bất đẳng thức như nào?
- Chứng minh bất đẳng thức bằng phương pháp đổi biến
- Bất đẳng thức Schur với t=1. Các kết quả hay sử dụng
- Sử dụng biểu thức phụ để tìm cực trị của biểu thức
- Chứng minh bất đẳng thức bằng phương pháp ghép cặp
- Ứng dụng Cosi ngược dấu chứng minh bất đẳng thức
- Cách chứng minh bất đẳng thức bằng vectơ
- Bất đẳng thức Côsi (Cauchy) và bài tập áp dụng
- Bất đẳng thức Bunhiacopxki và các kỹ thuật thường dùng
- Tuyển tập một số bài toán bất đẳng thức trong kì thi chuyên Toán 2020
- Bất đẳng thức Svac-xơ (bất đẳng thức cộng mẫu số)
Phương pháp đổi biến tỏ ra vô cùng hữu dụng với một số bài tập chứng minh bất đẳng thức. Cách đổi biến để chứng minh BĐT như nào?
Trong số các cách chứng minh bất đẳng thức cần phải học thì kỹ thuật đổi biến được sử dụng rất nhiều. Và dưới đây là phân loại các kiểu đổi biến.
a. Đổi biến các mẫu phức tạp
Trong một số bài toán mà biểu thức ở mẫu phức tạp thì việc đối biến đặc biệt có hiệu quả. Cụ thể chúng ta cùng đi xét các ví dụ dưới đây:
Ví dụ 1: Cho ![]()
Chứng minh rằng: ![]()
Hướng dẫn giải:
Ta đặt: 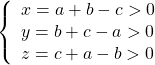
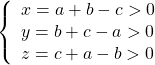
⇒ 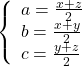
Ta cần chứng minh: ![]()
Ta có: ![]()
Mặt khác: ![]()
Từ đó ta được: ![]()
Từ (1) và (2) ta được: ![]()
Vậy: ![]()
Lời bình: Ta có thế đặt : ![]()
Khi đó: ![]()
Bài toán quy về chứng minh: ![]()
Ví dụ 2: Cho ![]() . Chứng minh rằng:
. Chứng minh rằng: ![]()
Hướng dẫn giải:
Ta đặt: ![]()
Khi đó: ![]()
Ta cần chứng minh: ![]()
![]()
Sử dụng bất đẳng thức AM-GM:
![]()
Vậy bất đẳng thức được chứng minh.
b. Đổi biến dựa trên giả thiết bài toán
Ví dụ 3: Cho ![]()
Chứng minh rằng: ![]()
Hướng dẫn giải:
Từ giả thiết ![]() ta đặt:
ta đặt: ![]()
Khi đó: ![]()
Tương tự có: ![]()
Ta cần chứng minh: ![]()
Ta đã biết: ![]()
Vậy bất đẳng thức được chứng minh.
Ví dụ 4: Cho ![]() và thỏa mãn
và thỏa mãn ![]()
Chứng minh rằng: ![]()
Hướng dẫn giải:
Từ giả thiết ta đặt: ![]()
Ta cần chứng minh: ![]()
Ta có: ![]()
Tương tự: ![]()
Cộng vế với vế được: ![]()
Đẳng thức xảy ra khi: ![]()
Ví dụ 5: Cho ![]() và
và ![]() Tim GTLN của
Tim GTLN của ![]()
(Trích đề thi HSG9, TP Hà Nội năm học 2018 – 2019)
Hướng dẫn giải:
Đặt: 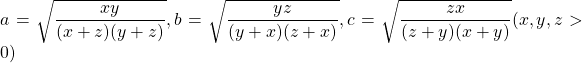
Ta có: ![]()
Mặt khác: ![]()
Từ đó: ![]()
Đẳng thức xảy ra khi: ![]()
Vậy: ![]()
c. Đổi biến p, q, r
Kiến thức cần nhớ.
Nếu ta đặt ![]() thì ta sẽ có các kết quả sau:
thì ta sẽ có các kết quả sau:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
Ngoài ra ta cũng thu được những đẳng thức quen thuộc dưới đây:
6) ![]()
7) ![]()
![]()
8) ![]()
9) ![]()
10) ![]()
Ví dụ 6: Cho ![]() và thỏa mãn
và thỏa mãn ![]()
Chứng minh rằng: ![]()
Hướng dẫn giải:
Theo kỹ thuật đổi biến p, q, r ta quy về bài toán sau:
Cho ![]() và thỏa mãn
và thỏa mãn ![]() . Chứng minh rằng:
. Chứng minh rằng: ![]()
Theo trên ta đã có: ![]()
Ta cần chứng minh:
![]()
Đẳng thức xảy ra tại: ![]()